From Hashes to Maps: Consistent Hashing as a Lesson in Go Internals

Ever wondered how system design concepts like consistent hashing actually works?? If you are one who loves exploring new buzzwords and read cool things at 2 am while scratching head then you’re most welcomed to this article.

This story starts back in last week when i read about consistent hashing in one of blogs then as usual i got curious how come this works? so like my ritual i went to youtube and searched about it and i found very interesting video of Arpit Bhayani(aka: Alsi Engineering) on Consistent Hashing and how Booking.com uses it at scale. This video opened my mind and i went back to my drawing board (wait do i have one? i mean escalidraw) then i started making diagram of whatsoever i have learned. By the time i was also reading some articles like bytebyteGo related to this.

After spending quite few days on passive learning i thought let’s try to implement whatever i can.

So as my go to language is Go these days, i went with that. That’s how all and i have implemented a bare bones(a tiny) naive way of consistent hashing in Go.

You guys must be thing what da f is consistent hashing why bro is repeating this word n time i mean whyyy?? To all fellow readers this is one of most important and highly used topic of distributed systems. So i will leave you guys with a space to learn more by own on this.

Hoping you all made till here means you already know a basic of what actually consistent hashing is.

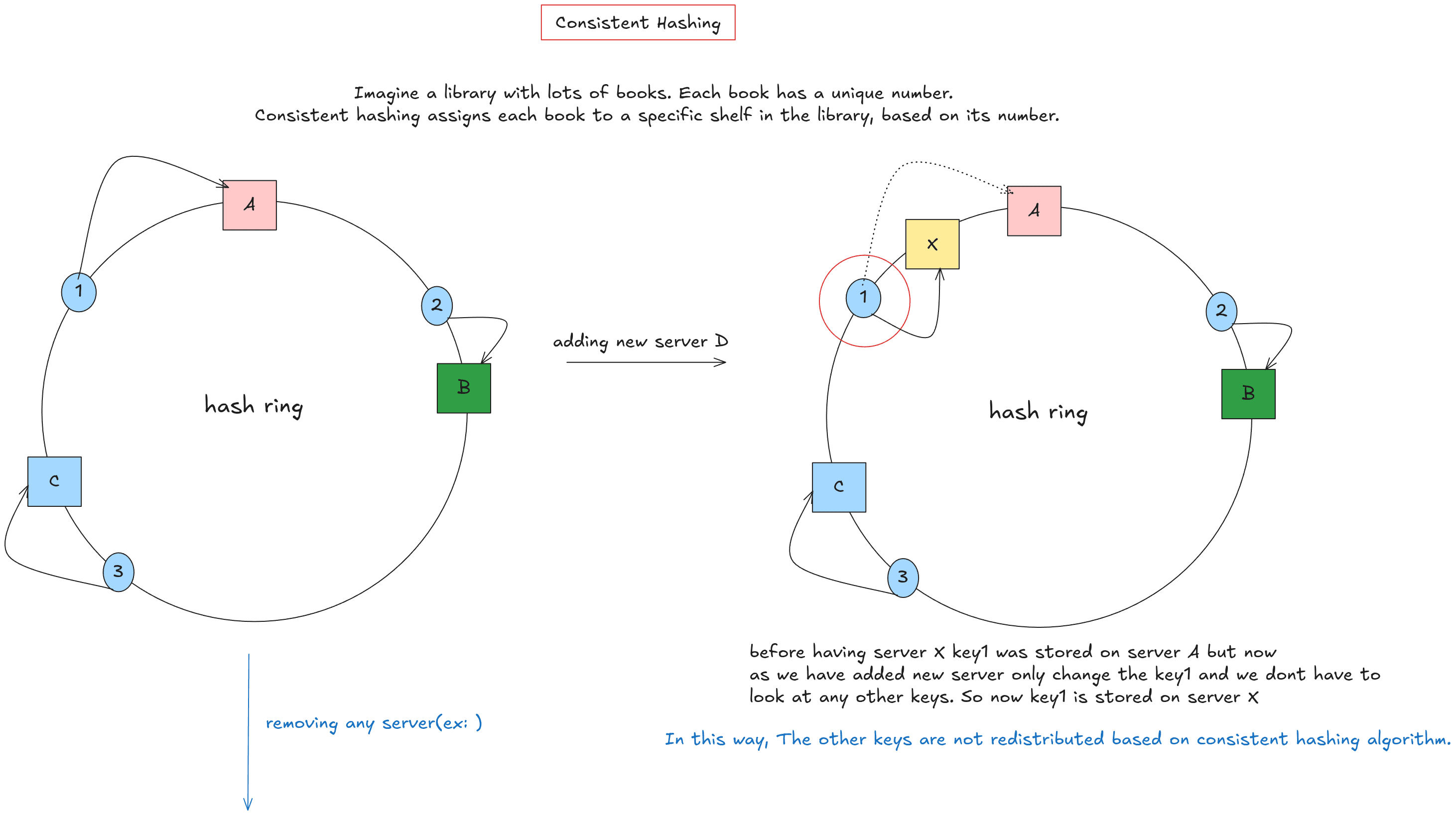
Let’s take a real life example: Suppose you have some books, and you are asked to place all those books on shelves.

Here’s a small twist: instead of arranging the shelves in a straight line, the shelves are arranged in a circular manner. Each book represents some data, and each shelf represents a server or cache node. Every server is placed at a certain ring on ring using some hash function so we call this ring as hash ring. We want to make system like when we add or remove server node(shelf) only small amount of data(books) must be reassigned.

This looks simple but it isn’t actually lets see how? So you have to built a robust system so that your lookup should be fast and there must be no data loss. Main problem i face in building this was choosing appropriate data structure, we can go with slice, maps so instead of normal map i went with sync Map in Go package sync.Map.

So this implementation basically uses two data structures one of it is this map by sync package and slice for storing sorted key of all server nodes. Here’s below how it looks.

type HashRing struct {
mu               sync.RWMutex
config           hashRingConfig
nodes            sync.Map
sortedKeyOfNodes []int64
}

hashRingConfig is basically a struct where we can choose which hash function we are using and mu is ReadWrite Mutex from sync package for locking ops.

Consistent Hashing mainly deals with two things:

1. Adding/Removing a server node.
2. Getting Data from minimal lookup in Hash RIng.

Main reason of choosing sync.Map is it provides us two different types of map internally one is normal hashmap called readMap and other is dirtyMap you can see that in go’s official source code.

So this a thread safe map and it provide us API’s like Load(), Store(), CompareAndDelete(), LoadAndDelete() so on.

Let’s dig deeper into readMap and dirty Map so read only map is an immutable map which can can be accessed without maintaining any locks. All Load operations are first checked in read only map which enables high lock free lookup reads. This map is optimized more for stable data which don’t change frequently and read frequently and write rarely which makes us use in hashing.

So about second map which is dirty map which is mutable map which is used to make writes. Store() API goes through this map internally. Dirty map don’t have in built concurrency feature but we leverage it concurrently by using external lock. It uses mutexes to avoid data race conditions.

ik this must be so much for beginner to digest but this is one of fundamental concept of concurrency for whoever worked in Go’s concurrent apis.

Once enough number of misses occurs then old dirty map is promoted to readOnly map and this is how old readOnly map becomes irrelevant for further lookups, Below is how it looks in Go’s source code.

type Map struct {
	mu Mutex
	read atomic.Pointer[readOnly]
	dirty map[any]*entry
	misses int
}

type readOnly struct {
	m       map[any]*entry
	amended bool // true if the dirty map contains some key not in m.
}

In short to summarize, sync.Map tries to keep the readonly map fast and lock-free, while the dirty map handles newer data, falling back to mutex locks in slow path.

“So the dirty map is an expanded key-value store of the readonly map?”(redis kinda)

Yes But not exactly,

The dirty map contains all the data from the readonly map, along with any new entries that haven’t yet been promoted to the readonly map. However, this doesn’t mean you need to update both maps separately when you change a value in the readonly map or dirty map.

That’s because Go doesn’t store your value type directly in the map. Instead, Go uses a pointer to an entry struct to hold the value, which looks like this:

type entry struct {
p atomic.Pointer[any]
}

The entry struct shown above has atomic.Pointer which points to actual data, So when you update a data you must’ve thought that you must update both maps manually but this is not how it works.

When you update a data you just have to update this pointer (p) since both readonly and dirty maps point to same entry pointer (p) your job gets done automatically, sounds cool right?

yes it is :)

This looks like a simple struct but here’s something interesting which Go does, the pointer behaves in three states: 1.Normal State 2.Delete State 3. Expunged Test

1. Normal State: This is when the entry is valid. The pointer p is pointing to a real value, and the entry exists in those maps, meaning it’s actively in use and can be read without any issues. This is an active state. Here both readOnly and dirty Map share same the same active entries, though it’s obvious that dirty Map contains more active entries than the read one. When we delete any active entry, then than entry moves to Delete state as mentioned below.

2. Deleted State: When an entry is deleted from a sync.Map, it’s not immediately removed from the readonly maps. Instead, the pointer p is simply set to nil, signaling that the entry has been deleted but still exists in the maps. Internally there’s some mechanism that moves all deleted entries into expunged state.

3. Expunged State: This is a special state where the key is fully removed. The entry is marked with a special sentinel value that indicates it’s been completely deleted. Once entries reach to expunged states that entries exists only in readOnly maps and not in dirty map but when we promote dirty Map into readOnly map then all these expunged entries are lost and completely removed.

So to summarize this all we can say a key can’t move directly from normal state to expunged state it has to move through deleted state first.

Let’s look now at how Load(), Store() and all common api’s works internally as we have used it in our consistent hashing implementation

1. Load(): Load is a one of API sync.Map provides us ready to use on Maps, it basically retrieves the value associated with the key if it exists. Load is designed in a way that it functions without a lock in a common case. Internally it checks readOnly map using an atomic pointer if we found and it is not deleted then immediately return value. If not found and ammended == false and return “not found”. If we don’t found and ammended == true then acquire a mutex and then start checking in the dirty map and increment the misses and whenever the threshold value of miss is crossed then dirty is promoted to next Read Map. In this way Load is extremely fast for in read-heavy workloads.

2. Store(): Store is used to insert or update a key-value pair. Unlike Load() Store comes up with locks via mutexes. Internally store loads readOnly map check if key exits and not expunged then update its value using atomic store and return immediately, Now if key is not their in readOnly map then Store aquires lock and recheck the read Map and if found now update value and return and unlock mutex. Lastly when dirty == nil it creates new dirty and copies all expunged values from readOnly map and set ammended = true, this now ensures that entries now go in dirty maps. This update or inserts new value in dirty map and unlocks the mutex.

This is how our two main api of sync.Map works internally. also we used LoadAndDelete() you can read about it in go package.

Now lets move to actual consistent hashing. wait what was above thing then? This was all build up !!

Consistent hashing is a technique used in distributed systems to distribute data across a dynamic set of nodes in a way that minimizes disruption when nodes are added or removed. The core problem it solves arises from naïve hashing approaches such as hash(key) % N, where N is the number of nodes. In such schemes, even a small change in the number of nodes causes almost all keys to be remapped to different nodes. This leads to massive data movement, cache invalidation, and performance degradation, which is unacceptable in large-scale systems.

Consistent hashing has become a foundational technique in modern distributed systems and is used in caches, databases, message queues, and load balancers. Systems such as distributed caches, NoSQL databases, and content delivery networks rely on it to scale horizontally while maintaining predictable behavior under change. Its main advantages are minimal data movement, deterministic routing, and resilience to node churn. However, it does introduce implementation complexity and requires careful tuning of virtual nodes and replication factors. But we are keeping virtual nodes on some other day.

This naive way of hashing is bad when you realize we are not uniformly distributing servers there must be a case where two servers must be so close or almost adjacent. In such cases one of them gets high load and becomes a SPOF (single point of failure).

So to summarize all the thing in consistent hashing we have to place servers in such a way that minimum data is distributed whenever some server is added or removed.

In our bare minimum implementations we have GetNode(), RemoveNode() and AddNode() methods used you can better see code in repo. Below image tells us how adding a new server in hash ring works.

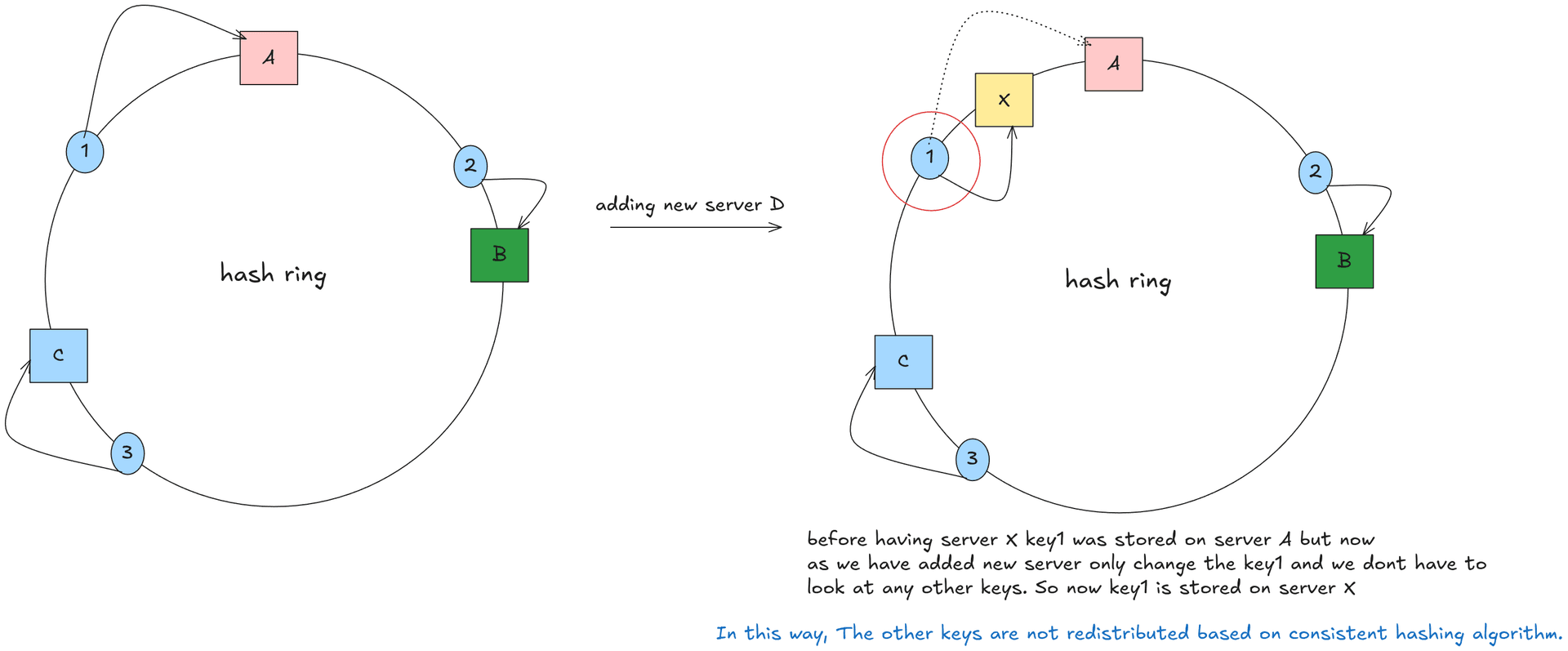
So you may notice why we have binarySearch named function in end let me tell you why? here binary search is needed because the hash space is ordered, and key lookup is fundamentally an order-based problem, not a direct index lookup like modulo hashing(due to which we needed consistent hashing). When both nodes and keys are placed on a hash ring, each node occupies a specific position in a large, continuous hash space. To determine which node should own a given key, the system must find the first node whose hash value is greater than or equal to the key’s hash, moving clockwise around the ring. This is essentially a “next greater element” problem in a sorted sequence.

In practice, the positions of nodes (or virtual nodes) on the ring are stored in a sorted data structure, such as a sorted slice or an ordered map. When a key arrives, its hash is computed, producing a number within the same hash space. The system then needs to locate the smallest node hash that is greater than or equal to the key’s hash. If such a node exists, it becomes the owner of the key; if it does not, the search wraps around to the first node in the sorted structure. Because the node positions are sorted, binary search is the most efficient way to perform this lookup.

Binary search is used because it reduces lookup time from linear to logarithmic complexity. Without binary search, the system would need to scan all node positions sequentially to find the next clockwise node, which would take O(N) time per lookup. In systems with hundreds or thousands of nodes or virtual nodes, this would add unacceptable latency. Binary search brings this down to O(log N), making consistent hashing viable for high-throughput systems where every request must be routed quickly.

Another important reason binary search fits naturally into consistent hashing is that node membership changes relatively infrequently compared to key lookups. Nodes are added or removed occasionally, at which point the sorted structure can be rebuilt or updated. Once the ring is sorted, it can be reused for millions of lookups. This asymmetry between frequent reads and infrequent writes makes a sorted array plus binary search an excellent trade-off between simplicity and performance. In our implementation binarySearch performs a binary search on the sortedKeyOfNodes slice to find the index of the first node hash that is greater than or equal to the given key hash. This implements the consistent hashing algorithm where keys are mapped to the first node whose hash is greater than or equal to the key's hash. If no such node exists (meaning the key hash is larger than all node hashes), it wraps around and returns index 0, implementing the ring behavior. Returns the index of the target node and nil error on success, or -1 and ErrNoConnectedNodes if the ring is empty.

Thats all i hope you understood this if not you can take pen paper and draw diagram and dry run this as a DSA problem.

So this is how by building consistent hashing in Go i have learned all this topics and used them which made me clear how systems actually behaves and what are tradeoffs and why we need systems that can bend but can’t break at scale.

By building this i explored depth in go’s sync.Map package and how it helps us and how using this we do concurrent addition and removal. Also a simply binary search which cram as pattern is highly important concept if we get into distributed systems and system designs.

as in our future improvements i will try to build new or add here a virtual nodes concept and will try to explain in some other blog. Thanks for reading, hope you enjoyed this one :)

Happy Learning Anon, Do Follow me on X/Medium wherever you are reading this !!